Fezzes are Cool, So is Math

So in keeping with the Doctor Who Halloween thread I figured I should post on Will’s costume of the 11th Doctor.  This one was super easy – we just bought a $10 tweed jacket from Savers, some suspenders and a bow tie that were on sale at Kohl’s, then made a fez out of scrap fabric, and Will added some aluminum foil (or aluminium foil for our British friends) to his battery operated toothbrush for a sonic screwdriver.  (I thought this was incredibly clever because it is indeed sonic.)

We weren’t going to make a fez for Will’s costume, but at the first party we went to someone told us how disappointed he was that Will was imitating the 11th Doctor without a fez.  So the next night (after drinking too many pumpkin beers) I decided to math one up.  I was really excited about it until I realized I did not remember how cones worked.  Luckily we found a website that made all my high school and college math classes obsolete!  There are lots of tutorials on making fezzes out there – but here is mine with some math!

I started with this picture of the doctor in his fez:

I then used paint.net to determine the height of the fez, and the diameter of the top and bottom of the fez in inches (not to scale).

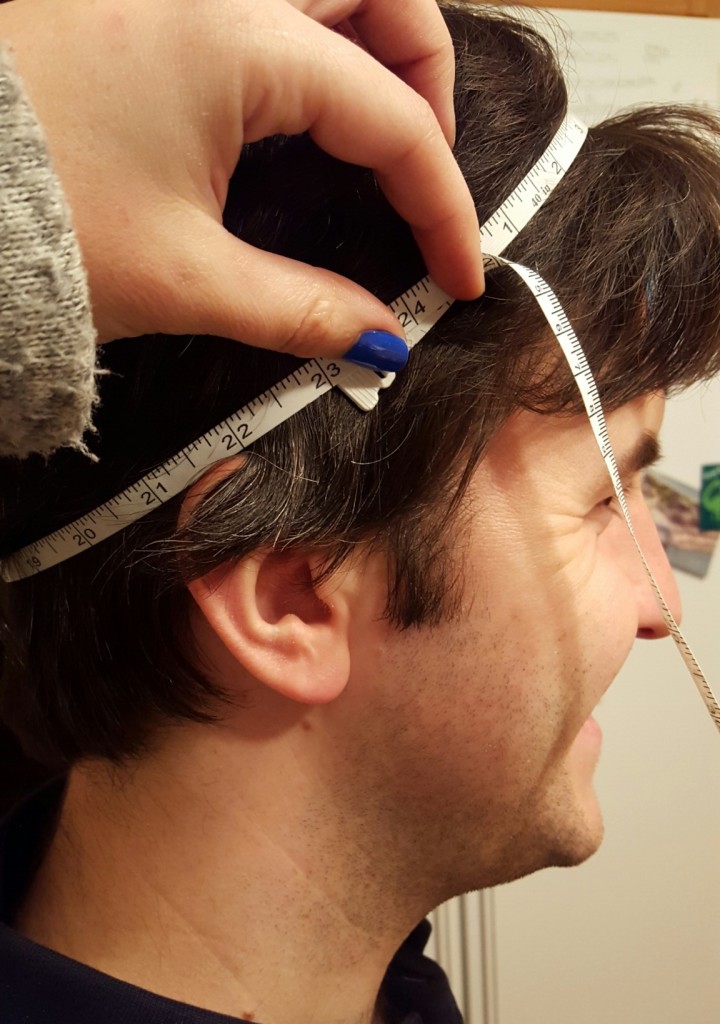
I then measured my husband’s head to determine the size of his fez (it was 24 inches):

He looks happy to be having his head measured.

From there I made some equalities from the picture:

Then I used my favorite 2nd grade math formula to find the circumference of the bottom of the fez (aka my husband’s head; C).:

I then solved for D and got my husband’s equivalent fez sizes:

Then here’s where things get fun.  The trick is to find the arc of a really large diameter circle that you can use to roll up into your fez (which is a cone with the top cut off). If you don’t want to know the math to do it, this calculator does it all for you… just plug it all in and skip to where you stop seeing equations.  Otherwise nerd out with me and the magic is below…

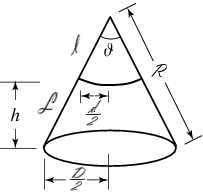
Here is a picture of the really large circle that you will cut an arc from and then roll up into a fez.  You ultimately need to find the value for R and l.  C, the arc length, is the circumference of my husband’s head, the only value we have established right now in this picture.

You can visualize the fez as a right cone with the top cut off.  You see here that the length of R from the circle is the length of the cone sides here:

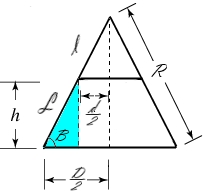
You can then visualize that cone as if you are viewing it straight on.  A cone in 2 dimensions is a triangle, so here’s what that looks like with the measurements transposed.  In this picture we have D and h already calculated.  I’ve also added an angle B that we’ll need to find R.

So first you’ll need to use the small (blue) triangle where we have two side values established to find the value of L the hypotenuse.  We can use the Pythagorean Theorem for this one:

So now that we have the value of L we can work on finding the value of R.  From the triangle picture we can see that the angle B forming the triangle containing L and h is the same angle as in the larger triangle containing R and D/2. So we solve for B using trig:

Since we have B, we can now use more trig to solve for R!

Then plug in and you’ll have your two values of interest, R and l!  Once you have those, you can measure out a string of length R and draw out part of a circle with it, and from the same focus you draw an arc using the shorter length l.  If you have a protractor you can use the following equation to figure out where to cut, but I just measured the arc length since I knew this value was the circumference of my husband’s head.

The rest was easy!  I cut out stiff fusible interfacing to the exact specifications of the arc segment pattern, and a circle with a radius of d/2.  I cut scrap fabric out 5/8 in larger than the two interfacing pieces and fused the interfacing to the wrong side of the fabric.

Then I sewed the cone segment (right sides together) down the side to form my fez, and attached the top (right sides together).  I snipped the top and and bottom fabric up to the interfacing to make it lay flat.  Finally a sewed a hem around the entire bottom of the hat.

That was it, about a 20 minute sewing project!  The math took more time than the sewing and cutting!

The Doctor